
Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 207 Макарычев — Подробные Ответы
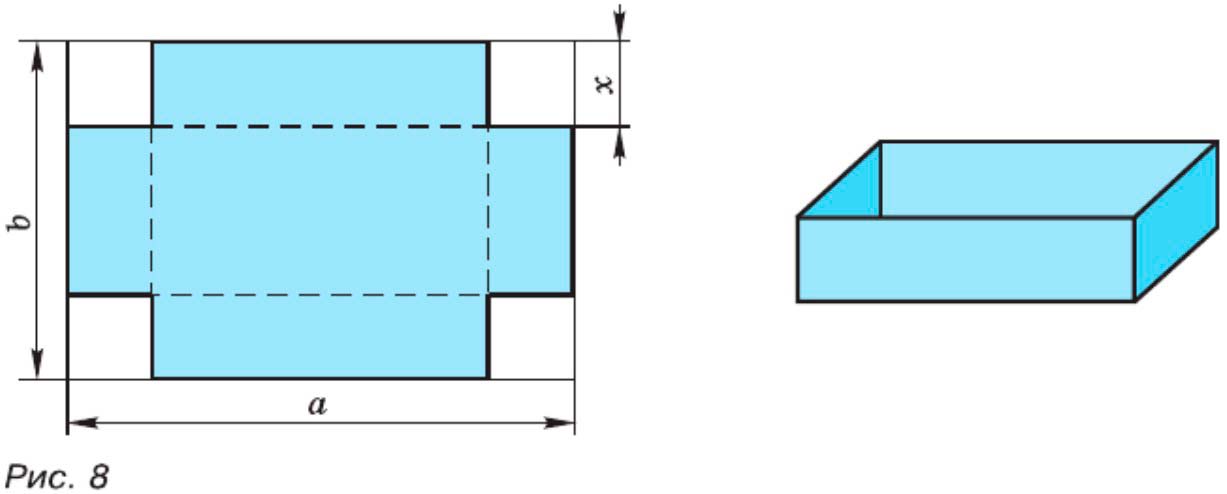
От прямоугольного листа картона со сторонами а см и b см отрезали по углам квадраты со сторонами х см (рис. 8). Из оставшейся части сделали открытую коробку. Запишите формулу для вычисления объёма V коробки. Вычислите по формуле объёма коробки, если а = 35, b = 25, х = 5. Какие значения может принимать переменна х при указанных значениях а и b?
\(
длина = a — 2x, \, ширина = b — 2x, \, высота = x
\)
\(
V = x(a — 2x)(b — 2x)
\)
\(
a = 35, \, b = 25, \, x = 5
\)
\(
V = 5(35 — 10)(25 — 10) = 5 \cdot 25 \cdot 15 = 1875 \, (\text{см}^3)
\)
\(
2x < b
\)
\(
0 < 2x < 25 \quad \Rightarrow \quad 0 < x < 12,5
\)
1. Формула для объёма коробки
После отрезания квадратов со стороной \(x\):
— Длина основания коробки становится равной \(a — 2x\) (так как с двух сторон отрезали по \(x\)).
— Ширина основания коробки становится равной \(b — 2x\) (по той же причине).
— Высота коробки равна \(x\), так как именно на такую высоту подняты боковые стороны.
Объём прямоугольной коробки рассчитывается по формуле:
\(V = \text{длина} \cdot \text{ширина} \cdot \text{высота}\).
Подставляем выражения для длины, ширины и высоты:
\(V = x(a — 2x)(b — 2x)\).
2. Вычисление объёма коробки при \(a = 35\), \(b = 25\), \(x = 5\)
Подставим значения в формулу:
\(V = x(a — 2x)(b — 2x)\).
\(V = 5(35 — 2 \cdot 5)(25 — 2 \cdot 5)\).
\(V = 5(35 — 10)(25 — 10)\).
\(V = 5 \cdot 25 \cdot 15\).
\(V = 1875 \, \text{см}^3\).
Таким образом, объём коробки равен \(1875 \, \text{см}^3\).
3. Определение допустимых значений переменной \(x\)
Для того чтобы из картона можно было вырезать квадраты и изготовить коробку, необходимо, чтобы:
— Длина основания коробки была больше нуля: \(a — 2x > 0\).
— Ширина основания коробки была больше нуля: \(b — 2x > 0\).
Рассмотрим каждое условие:
\(a — 2x > 0 \quad \Rightarrow \quad x < \frac{a}{2}\).
\(b — 2x > 0 \quad \Rightarrow \quad x < \frac{b}{2}\).
Так как оба условия должны выполняться одновременно, берём более строгое из них:
\(x < \min\left(\frac{a}{2}, \frac{b}{2}\right)\).
Подставляем значения \(a = 35\), \(b = 25\):
\(\frac{a}{2} = \frac{35}{2} = 17,5\), \(\frac{b}{2} = \frac{25}{2} = 12,5\).
Следовательно, \(x < 12,5\).
Кроме того, очевидно, что \(x > 0\), так как сторона квадрата не может быть отрицательной или равной нулю.
Итак, переменная \(x\) может принимать значения в интервале:
\(0 < x < 12,5\).
Ответ:
1. Формула для объёма: \(V = x(a — 2x)(b — 2x)\).
2. При \(a = 35\), \(b = 25\), \(x = 5\): объём коробки равен \(1875 \, \text{см}^3\).
3. Допустимые значения переменной \(x\): \(0 < x < 12,5\).



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!