ГДЗ по Алгебре 7 Класс Номер 346 Макарычев — Подробные Ответы

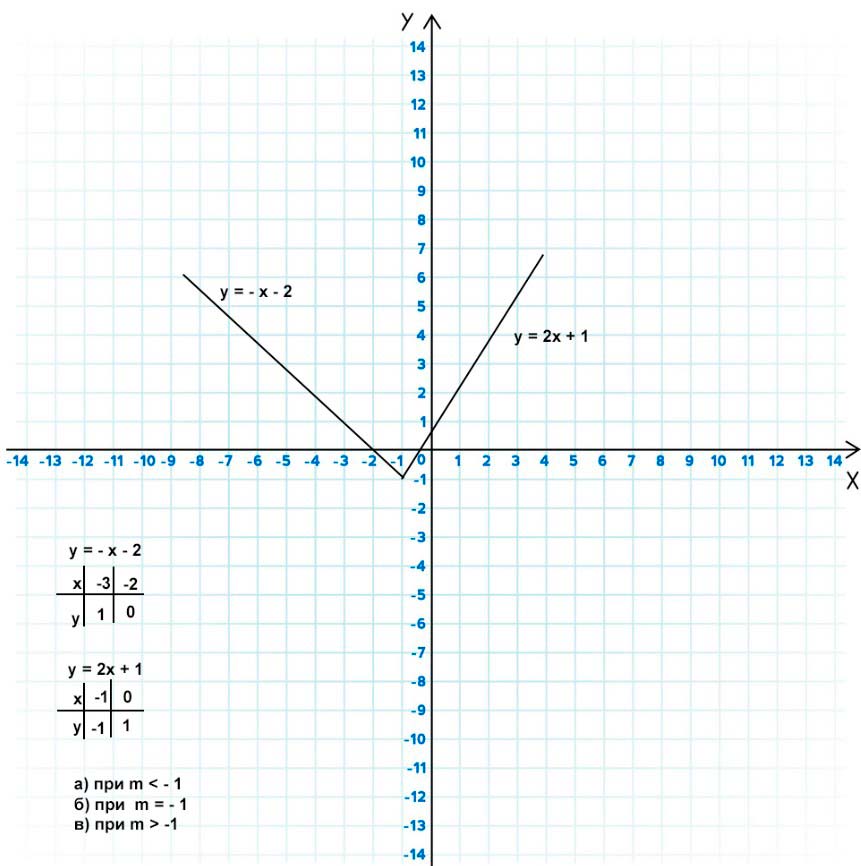
Постройте график функции

\(
y =
\begin{cases}
-x — 2, & \text{если } x < -1, \\
2x + 1, & \text{если } x \geq -1.
\end{cases}
\)

Определите, при каких значениях m прямая y = m и график данной функции:
а) не имеют общих точек;
б) имеют ровно одну общую точку;
в) имеют ровно две общие точки.

1. Разделение на части
Функция состоит из двух кусков:

1. \( y = -x — 2 \), если \( x < -1 \);
2. \( y = 2x + 1 \), если \( x \geq -1 \).

2. Анализ первого кусочка: \( y = -x — 2 \), если \( x < -1 \)

— Это линейная функция с угловым коэффициентом \( -1 \), что означает, что график убывает.
— Свободный член \( -2 \) задает начальное смещение графика вниз.

Построение:
1) Выберем несколько точек для \( x < -1 \):
— Если \( x = -2 \): \( y = -(-2) — 2 = 2 — 2 = 0 \).
— Если \( x = -3 \): \( y = -(-3) — 2 = 3 — 2 = 1 \).
— Если \( x = -4 \): \( y = -(-4) — 2 = 4 — 2 = 2 \).

2) Эта часть функции действует только для \( x < -1 \).
Например, при \( x = -1 \):
\( y = -(-1) — 2 = 1 — 2 = -1 \).
Однако эта точка не включается в график, так как \( x < -1 \).

3. Анализ второго кусочка: \( y = 2x + 1 \), если \( x \geq -1 \)

— Это линейная функция с угловым коэффициентом \( 2 \), что означает, что график возрастает.
— Свободный член \( +1 \) задает начальное смещение графика вверх.

Построение:
1) Выберем несколько точек для \( x \geq -1 \):
— Если \( x = -1 \): \( y = 2(-1) + 1 = -2 + 1 = -1 \).
— Если \( x = 0 \): \( y = 2(0) + 1 = 0 + 1 = 1 \).
— Если \( x = 1 \): \( y = 2(1) + 1 = 2 + 1 = 3 \).

2) Эта часть функции действует только для \( x \geq -1 \).
Например, при \( x = -1 \):
\( y = -1 \). Эта точка включается в график, так как \( x \geq -1 \).

4. Сборка графика

Теперь объединим обе части:

1) Первая часть (\( y = -x — 2 \), если \( x < -1 \)):
Точки: \( (-2, 0), (-3, 1), (-4, 2) \).
График — прямая линия, убывающая слева от \( x = -1 \).

2) Вторая часть (\( y = 2x + 1 \), если \( x \geq -1 \)):
Точки: \( (-1, -1), (0, 1), (1, 3) \).
График — прямая линия, возрастающая справа от \( x = -1 \).

5. Особенность соединения в точке \( x = -1 \)

Для \( x = -1 \):
Первая часть (\( y = -x — 2 \)) дает \( y = -1 \), но эта точка не включается, так как \( x < -1 \).
Вторая часть (\( y = 2x + 1 \)) дает \( y = -1 \), и эта точка включается, так как \( x \geq -1 \).

Таким образом, график непрерывен в точке \( x = -1 \), но имеет разрыв в области определения.

6. Итоговый график

Нарисуйте оси координат.
Отметьте точки, рассчитанные выше.
Проведите прямую линию для каждой части функции, учитывая область определения:
Для \( x < -1 \): график убывает.
Для \( x \geq -1 \): график возрастает.

а) Прямая \( y = m \) и график не имеют общих точек

Для отсутствия общих точек прямая \( y = m \) должна проходить в области, где ни одна из частей функции не достигает значения \( m \).

Первая часть (\( y = -x — 2 \)) достигает минимального значения \( y = -1 \) при \( x = -1 \).
Вторая часть (\( y = 2x + 1 \)) достигает минимального значения \( y = -1 \) при \( x = -1 \).

Следовательно, если \( m < -1 \), прямая \( y = m \) не пересекает ни одну часть графика.

Ответ: \( m < -1 \).

б) Прямая \( y = m \) имеет ровно одну общую точку

Прямая \( y = m \) имеет ровно одну общую точку, если она касается графика функции в точке разрыва, то есть в точке \( x = -1 \).

В точке \( x = -1 \) график функции принимает значение \( y = -1 \).
Если \( m = -1 \), то прямая \( y = -1 \) проходит через точку разрыва графика и пересекает его ровно в одной точке.

Ответ: \( m = -1 \).

в) Прямая \( y = m \) имеет ровно две общие точки

Прямая \( y = m \) имеет две общие точки, если она пересекает обе части графика функции:

Пересечение с первой частью (\( y = -x — 2 \)) происходит, если \( m > -1 \).
Пересечение со второй частью (\( y = 2x + 1 \)) также происходит, если \( m > -1 \).

Таким образом, при \( m > -1 \) прямая \( y = m \) пересекает график функции в двух точках.

Ответ: \( m > -1 \).