
Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 49 Макарычев — Подробные Ответы
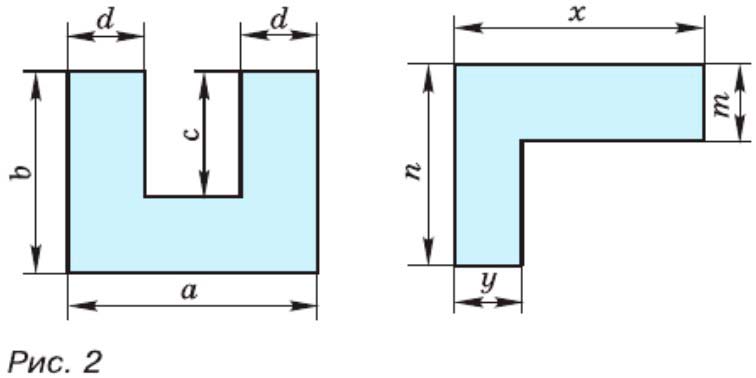
На рисунке 2 указаны длины отрезков (в сантиметрах). Для каждой фигуры составьте выражение для вычисления её площади (в квадратных сантиметрах).
+---+ +---+ +-------+ | | | | | | | | | | | | | +-------+ | | +---+ | | | | | | | | +---------------+ +---+
Обозначения для первой фигуры:
— Ширина верхних выступов: \( d \)
— Высота внутреннего выреза: \( c \)
— Общая ширина: \( a \)
— Общая высота: \( b \)
Обозначения для второй фигуры:
— Горизонтальная длина: \( x \)
— Вертикальная длина: \( n \)
— Ширина горизонтальной части: \( m \)
— Ширина вертикальной части: \( y \)
1) ab – c · (a – 2d) — площадь первой фигуры
2) xm + y · (n – m) – площадь второй фигуры
1. U-образная фигура
Формула для площади первой фигуры:
\( S_{\text{U}} = ab — c \cdot (a — 2d) \)
Шаг 1. Общая площадь прямоугольника
Общая площадь фигуры без выреза равна площади большого прямоугольника:
\( S_{\text{общ}} = a \cdot b \)
где:
— \( a \) — общая ширина фигуры,
— \( b \) — общая высота фигуры.
Шаг 2. Площадь выреза
Площадь выреза — это площадь внутреннего прямоугольника:
\( S_{\text{вырез}} = c \cdot (a — 2d) \)
где:
— \( a — 2d \) — ширина выреза (общая ширина минус два выступа по \( d \)),
— \( c \) — высота выреза.
Шаг 3. Площадь U-образной фигуры
Чтобы найти площадь U-образной фигуры, нужно из общей площади вычесть площадь выреза:
\( S_{\text{U}} = S_{\text{общ}} — S_{\text{вырез}} \)
Подставляем выражения:
\( S_{\text{U}} = a \cdot b — c \cdot (a — 2d) \)
2. Угловая фигура
Формула для площади второй фигуры:
\( S_{\text{угловая}} = x \cdot m + y \cdot (n — m) \)
Шаг 1. Площадь горизонтального прямоугольника
Горизонтальный прямоугольник (верхняя часть фигуры) имеет площадь:
\( S_{\text{горизонт}} = x \cdot m \)
где:
— \( x \) — длина горизонтальной части,
— \( m \) — ширина горизонтальной части.
Шаг 2. Площадь вертикального прямоугольника
Вертикальный прямоугольник (левая часть фигуры) имеет площадь:
\( S_{\text{вертик}} = y \cdot n \)
Однако из этой площади нужно вычесть часть, которая пересекается с горизонтальной частью. Пересечение — это прямоугольник с размерами \( y \cdot m \). Поэтому корректируем площадь вертикального прямоугольника:
\( S_{\text{вертик}} = y \cdot (n — m) \)
где:
— \( n — m \) — высота вертикальной части без учета пересечения.
Шаг 3. Суммарная площадь угловой фигуры
Складываем площади горизонтального и скорректированного вертикального прямоугольников:
\( S_{\text{угловая}} = x \cdot m + y \cdot (n — m) \)



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!