Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 326 Макарычев — Подробные Ответы
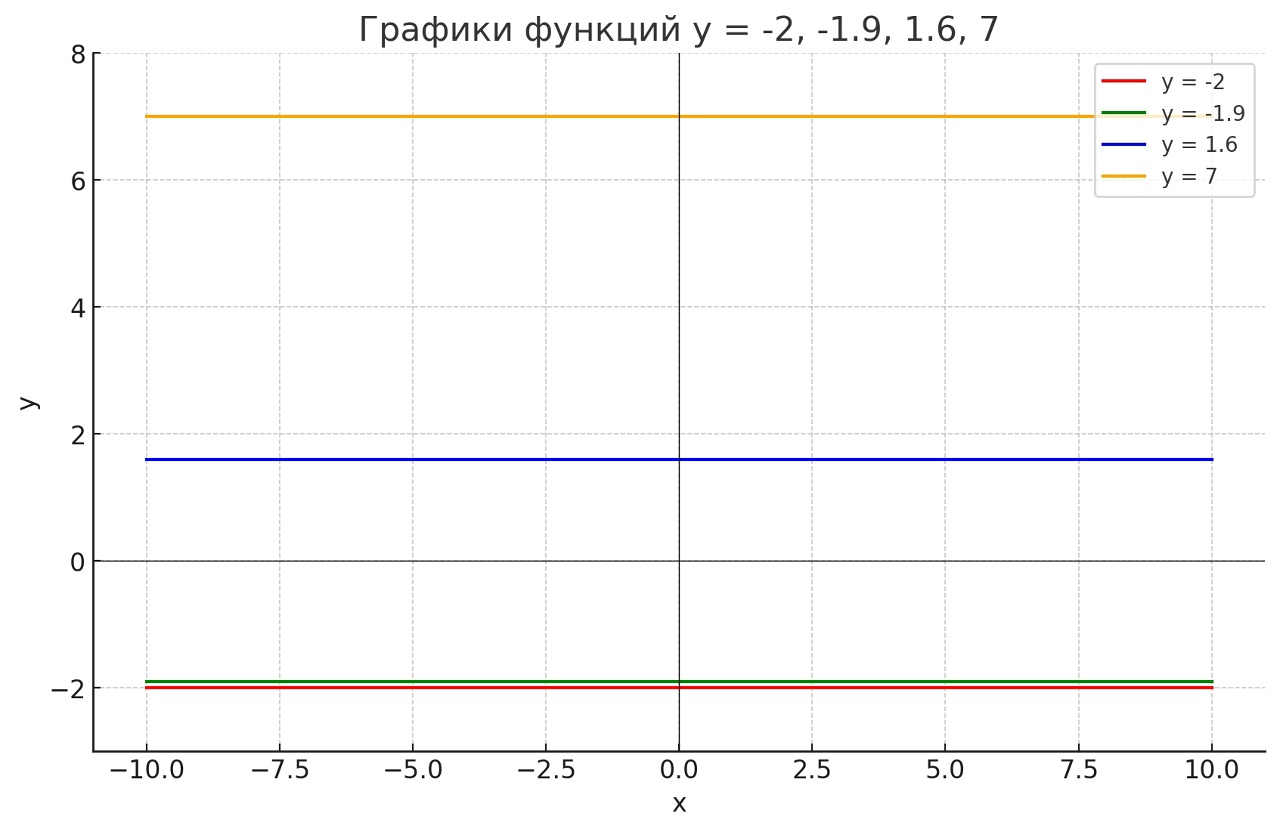
Постройте графики функций у = −2, у = −1,9, у = 1,6, у = 7.
Чтобы построить графики функций \( y = -2 \), \( y = -1.9 \), \( y = 1.6 \), \( y = 7 \), нужно понимать, что каждая из этих функций представляет собой линейную функцию, где значение \( y \) остается постоянным для любого значения \( x \). Это означает, что графиком каждой функции будет прямая линия, параллельная оси \( x \).
Шаги для построения графиков:
1. Определение функции
Каждая из данных функций имеет вид \( y = c \), где \( c \) — это константа. Это говорит о том, что значение \( y \) фиксировано и не зависит от значения \( x \). Например:
— Для функции \( y = -2 \), значение \( y \) всегда равно -2.
— Для функции \( y = -1.9 \), значение \( y \) всегда равно -1.9.
— Для функции \( y = 1.6 \), значение \( y \) всегда равно 1.6.
— Для функции \( y = 7 \), значение \( y \) всегда равно 7.
2. Построение каждой линии
Для построения графика нужно выбрать несколько точек на оси \( x \) (например, \( x = -5, -3, 0, 2, 5 \)) и для каждого значения \( x \) установить соответствующее значение \( y \), которое остается постоянным.
— Функция \( y = -2 \):
— Точки: (-5, -2), (-3, -2), (0, -2), (2, -2), (5, -2).
— Соединяем точки прямой линией, параллельной оси \( x \).
— Функция \( y = -1.9 \):
— Точки: (-5, -1.9), (-3, -1.9), (0, -1.9), (2, -1.9), (5, -1.9).
— Соединяем точки прямой линией.
— Функция \( y = 1.6 \):
— Точки: (-5, 1.6), (-3, 1.6), (0, 1.6), (2, 1.6), (5, 1.6).
— Соединяем точки прямой линией.
— Функция \( y = 7 \):
— Точки: (-5, 7), (-3, 7), (0, 7), (2, 7), (5, 7).
— Соединяем точки прямой линией.
3. Размещение линий на координатной плоскости
На координатной плоскости:
— Линия для \( y = -2 \) будет проходить ниже оси \( x \), на уровне \( y = -2 \).
— Линия для \( y = -1.9 \) будет чуть выше линии \( y = -2 \).
— Линия для \( y = 1.6 \) будет выше оси \( x \), на уровне \( y = 1.6 \).
— Линия для \( y = 7 \) будет значительно выше оси \( x \), на уровне \( y = 7 \).
Графики будут выглядеть как набор горизонтальных линий на разных уровнях оси \( y \).
Алгебра
