
Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 347 Макарычев — Подробные Ответы
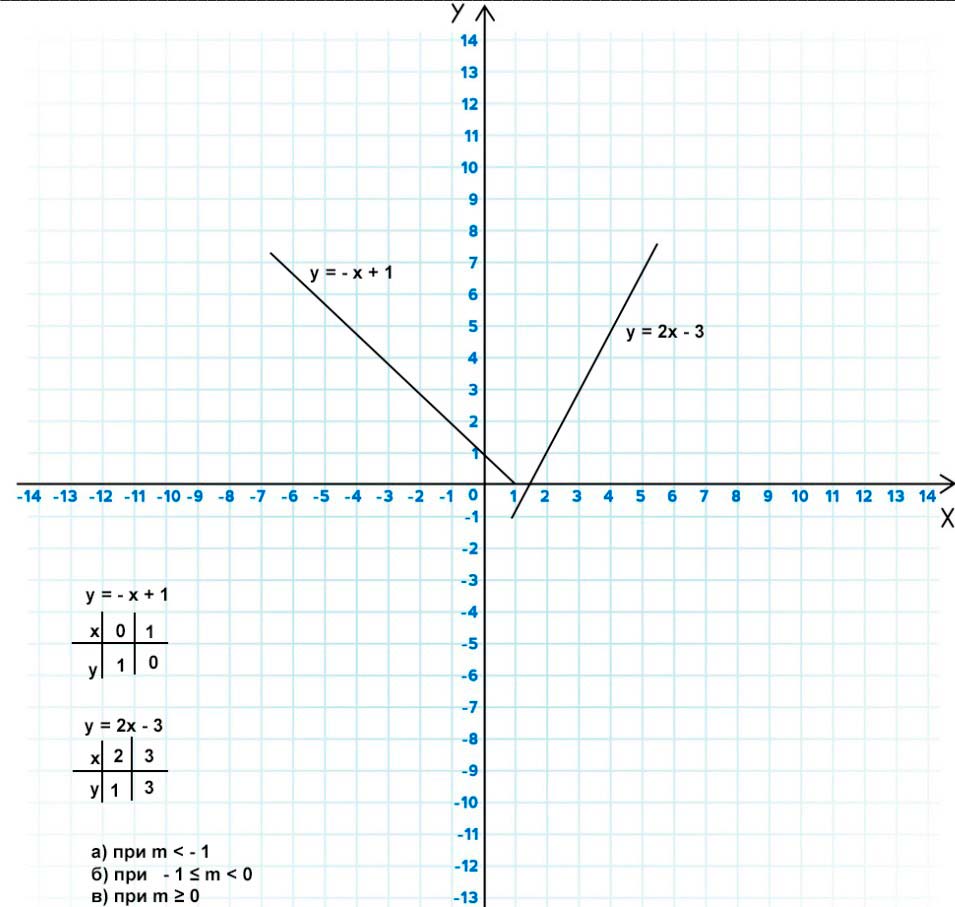
Постройте график функции
\(
y = \begin{cases}
-x + 1, & \text{если } x \leq 1, \\
2x — 3, & \text{если } x > 1.
\end{cases}
\)
Определите, при каких значениях m прямая y = m и график данной функции:
а) не имеют общих точек;
б) имеют одну общую точку;
в) имеют две общие точки.
Для построения графика функции \( y = \begin{cases} -x + 1, & \text{если } x \leq 1, \\ 2x — 3, & \text{если } x > 1. \end{cases} \) разобьем задачу на несколько шагов.
1. Разберем функцию по частям
Функция состоит из двух кусков:
1) \( y = -x + 1 \), если \( x \leq 1 \).
Это линейная функция с отрицательным углом наклона (\( -1 \)) и пересечением с осью \( y \) в точке \( (0, 1) \).
График этой функции — прямая линия, которая убывает слева от точки \( x = 1 \).
2) \( y = 2x — 3 \), если \( x > 1 \).
Это линейная функция с положительным углом наклона (\( 2 \)) и пересечением с осью \( y \) в точке \( (0, -3) \).
График этой функции — прямая линия, которая возрастает справа от точки \( x = 1 \).
2. Найдем ключевые точки
Для построения графика нужно определить несколько ключевых точек для каждой части функции.
Часть 1: \( y = -x + 1 \), если \( x \leq 1 \)
— При \( x = 0 \):
\( y = -0 + 1 = 1 \).
Точка: \( (0, 1) \).
— При \( x = 1 \):
\( y = -1 + 1 = 0 \).
Точка: \( (1, 0) \).
График этой части — прямая линия, проходящая через точки \( (0, 1) \) и \( (1, 0) \).
Часть 2: \( y = 2x — 3 \), если \( x > 1 \)
— При \( x = 2 \):
\( y = 2 \cdot 2 — 3 = 4 — 3 = 1 \).
Точка: \( (2, 1) \).
— При \( x = 3 \):
\( y = 2 \cdot 3 — 3 = 6 — 3 = 3 \).
Точка: \( (3, 3) \).
График этой части — прямая линия, проходящая через точки \( (2, 1) \) и \( (3, 3) \).
3. Учитываем разрыв в точке \( x = 1 \)
— В точке \( x = 1 \) функция меняет свое выражение.
— Для \( x = 1 \), значение функции по первой части (\( y = -x + 1 \)) равно \( y = 0 \).
— Для \( x = 1 \), значение функции по второй части (\( y = 2x — 3 \)) равно \( y = -1 \).
Таким образом, в точке \( x = 1 \) на графике будет разрыв:
— Точка \( (1, 0) \) принадлежит первой части графика.
— Точка \( (1, -1) \) принадлежит второй части графика.
4. Построение графика
Теперь мы можем построить график:
1. Нарисуем часть \( y = -x + 1 \) для \( x \leq 1 \).
Это прямая, проходящая через точки \( (0, 1) \) и \( (1, 0) \).
2. Нарисуем часть \( y = 2x — 3 \) для \( x > 1 \).
Это прямая, проходящая через точки \( (2, 1) \) и \( (3, 3) \).
3. Укажем разрыв в точке \( x = 1 \):
— Точка \( (1, 0) \) принадлежит первой части графика.
— Точка \( (1, -1) \) принадлежит второй части графика.
5. Итоговый график
— Левая часть графика (\( x \leq 1 \)) — убывающая прямая, заканчивающаяся в точке \( (1, 0) \).
— Правая часть графика (\( x > 1 \)) — возрастающая прямая, начинающаяся в точке \( (1, -1) \).
— Между двумя частями есть разрыв в точке \( x = 1 \).
а) Когда прямая \( y = m \) не имеет общих точек с графиком функции?
Прямая \( y = m \) не будет пересекать график функции, если \( m \) находится ниже самой нижней точки графика.
— Самая нижняя точка графика:
— Для \( y = -x + 1 \): на промежутке \( x \leq 1 \) значение \( y \) убывает и достигает минимального значения \( y = 0 \) при \( x = 1 \).
— Для \( y = 2x — 3 \): на промежутке \( x > 1 \) значение \( y \) возрастает, начиная с \( y = -1 \) при \( x = 1 \).
Итак, самая нижняя точка графика — это \( y = -1 \), которая достигается при \( x = 1 \) для \( y = 2x — 3 \).
— Условие:
Прямая \( y = m \) не имеет общих точек с графиком функции, если \( m < -1 \).
б) Когда прямая \( y = m \) имеет одну общую точку с графиком функции?
Прямая \( y = m \) будет касаться графика функции в одной точке, если:
— Она проходит через точку разрыва графика (в точке \( x = 1 \)), где значения \( y \) переходят от \( y = 0 \) (для \( y = -x + 1 \)) к \( y = -1 \) (для \( y = 2x — 3 \)).
— Это происходит, если \( m \) находится между \( -1 \) и \( 0 \), то есть \( -1 \leq m < 0 \).
в) Когда прямая \( y = m \) имеет две общие точки с графиком функции?
Прямая \( y = m \) пересекает график функции в двух точках, если:
— Она проходит выше самой нижней точки графика (\( y = -1 \)).
— При этом \( m \geq 0 \), так как график функции состоит из двух частей, каждая из которых возрастает или убывает, обеспечивая два пересечения.
— Условие:
Прямая \( y = m \) имеет две общие точки с графиком функции, если \( m \geq 0 \).



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!