Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 408 Макарычев — Подробные Ответы
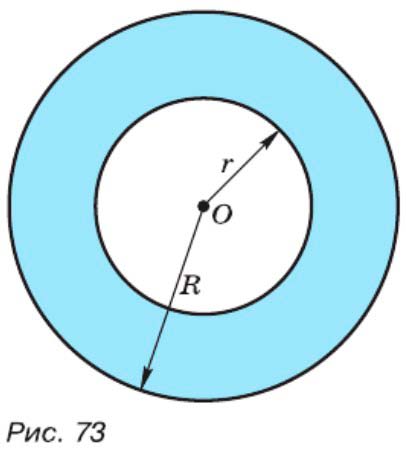
Составьте формулу для вычисления площади кольца, изображённого на рисунке 73. Найдите площадь кольца, если R = 6,4 см, r = 3,6 см.
S = πR² — πr² = π(R² — r²)
R = 6,4 см r = 3,6 см
S = 3,14(40,96 — 12,96) = 3,14·28 = 87,92 (см²)
1. Понимание задачи
Кольцо, которое мы рассматриваем, состоит из двух концентрических окружностей (окружностей с общим центром), где:
— Внешняя окружность имеет радиус \( R \).
— Внутренняя окружность имеет радиус \( r \).
Площадь кольца — это площадь, заключённая между этими двумя окружностями. Чтобы найти эту площадь, мы вычтем площадь внутреннего круга из площади внешнего круга.
2. Формула для площади кольца
Площадь круга вычисляется по формуле:
\( S = \pi \times \text{(радиус)}^2 \)
Таким образом:
— Площадь внешнего круга с радиусом \( R \) равна \( \pi R^2 \).
— Площадь внутреннего круга с радиусом \( r \) равна \( \pi r^2 \).
Площадь кольца будет разностью этих площадей:
\( S = \pi R^2 — \pi r^2 \)
Эту формулу можно упростить, вынеся \( \pi \) за скобки:
\( S = \pi (R^2 — r^2) \)
3. Подстановка значений
Теперь подставим в формулу конкретные значения радиусов:
— \( R = 6,4 \, \text{см} \)
— \( r = 3,6 \, \text{см} \)
Вычисления:
\( R^2 = (6,4)^2 = 40,96 \)
\( r^2 = (3,6)^2 = 12,96 \)
\( R^2 — r^2 = 40,96 — 12,96 = 28 \)
\( S = \pi (R^2 — r^2) = 3,14 \times 28 = 87,92 \, \text{см}^2 \)
Ответ:
\( S = 87,92 \, \text{см}^2 \)
Алгебра
