Учебник Ю.Н. Макарычева «Алгебра 7 класс» давно зарекомендовал себя как одно из лучших пособий по алгебре, которое одинаково эффективно помогает ученикам освоить сложные темы, а учителям — грамотно организовать уроки.
Ключевые преимущества учебника:
1. Продуманная структура — от теории с понятными объяснениями и примером применения до практических заданий.
2. Широкий выбор заданий — от лёгких упражнений до задач, развивающих аналитическое мышление.
3. Практическая ценность— задачи с опорой на жизненные ситуации делают материал ближе к реальности.
4. Подробные объяснения— пошаговая подача сложных тем облегчает освоение ключевых концепций.
5. Экзаменационный тренинг — в конце разделов представлены задания для подготовки к контрольным работам.
Пособие Макарычева не только учит математике, но также развивает логику, аналитическое мышление и целеустремлённость. Для успешного изучения алгебры и уверенного выполнения задач этот учебник станет идеальным выбором.
ГДЗ по Алгебре 7 Класс Номер 50 Макарычев — Подробные Ответы
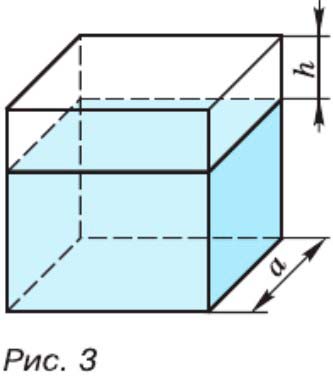
Ребро куба равно а м. От этого куба отрезан прямоугольный параллелепипед, высота которого равна h м (рис. 3). Найдите объём оставшейся части.
Vк = a³
Vп = a · a · h = a²h (м³)
Vu = a³ — a²h = a²(a — h) (м³)
Для решения задачи найдем объём оставшейся части куба после того, как от него отрезали прямоугольный параллелепипед. Объясним каждый шаг подробно.
1. Объём исходного куба
Куб — это фигура, у которой все ребра равны. Если длина ребра куба равна \( a \), то его объём \( Vk \) находится по формуле:
\( Vk = a^3 \)
Это объём всего куба до отрезания.
2. Объём отрезанного параллелепипеда
Прямоугольный параллелепипед имеет объём, равный произведению его длины, ширины и высоты. Длина и ширина параллелепипеда равны \( a \) (так как его основания совпадают с основанием куба), а высота равна \( h \). Объём \( Vp \) параллелепипеда:
\( Vp = a \cdot a \cdot h = a^2h \)
3. Объём оставшейся части
Чтобы найти объём оставшейся части \( Vu \), нужно из объёма куба \( Vk \) вычесть объём отрезанного параллелепипеда \( Vp \):
\( Vu = Vk — Vp \)
Подставляем значения:
\( Vu = a^3 — a^2h \)
4. Упрощение формулы
Объём оставшейся части можно записать в виде:
\( Vu = a^2(a — h) \)
Ответ:
Объём оставшейся части равен:
\( Vu = a^2(a — h) \)
Алгебра
